Bayesian Inference with Probabilisitc Pupulation Codes

[  BiologicalComplexity  ] 23 Apr 2021

This is a summary about paper Ma, Wei Ji, et al. (2006) Bayesian inference with probabilistic population codes. Nature neuroscience and Ma, Wei Ji, et al. (2014) Neural Coding of Uncertainty and Probability. Annual Review of Neuroscience. The authors presented a model, with some physiological evidence, about neural realization of bayesian probabilitic computation in human brains: probabilistic population codes. This report borrows a lot from Yafah’s presentation.

So what does it mean by bayesian inference in Human brain? For example, visual signals are degraded in the dark, other individuals’ internal states are not directly accessible, and the amount of food available in food sources may vary depending on many unknown factors. So generally speaking, when making decisions, humans have to take into account various information and uncertainty to make guesses and adjust confidences. This can be described formally through Bayesian Inference, that is, given some event \(s\) and evidence \(r\):

\[p(s | \mathbf{r}) \propto p(\mathbf{r} | s) p(s)\]

It turns out humans perform such Bayesian Inference correctly (successfully get the optimal way) and optimally perform at certain tasks such as integrating visual and haptic feedback to estimate height. But this observation seems contradictory to the neural variablility from the experiments: Neurons have highly variable responses: the behavior of neurons changes dramatically from trial to trial in tests; This unpredictability would seem to lend itself badly to implementing near optimal bayesian inference, which would intuitively require stable and deterministic behavior. This paper attempted to resolve that paradox and show that actually there are natrual and elegant ways to implement and view bayesian inference with neurons.

The first idea is: distribution instead of values, which means the activity of populations of neurons in encoding a probability distributions instead of values of different variables. Such ways of using populations of neurons allows us to use the variability of individual neurons to our advantage. They called it Probabilisitc Population Codes(PPC). As shown in the following picture, the response of a population of neurons to a single stimuli can encode a full distribution:

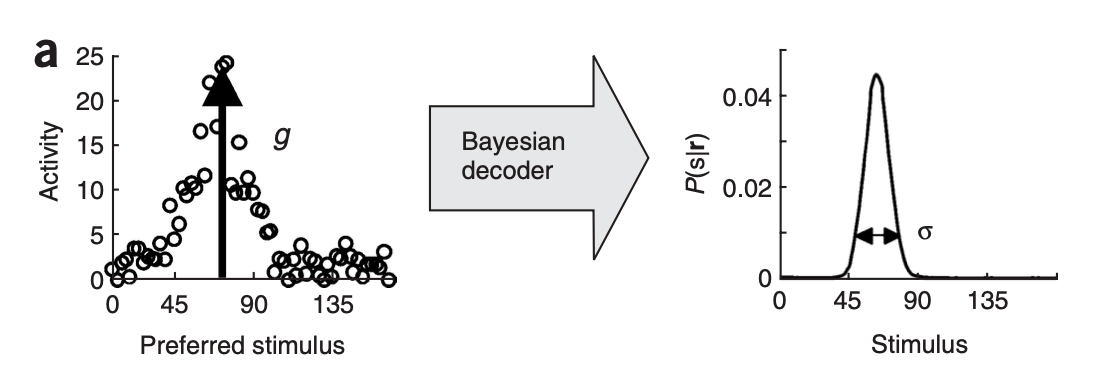
Such reformation also provides a possibility to interprete with Bayes theorem. So how can we apply such framework in Bayesian Inference?

The authors adopted the idea of “Cue Combination”: In a cue combination task, one’s goal is to take as input two cues and use this to make an inference about a stimulus. For instance, one study cited by the paper did this with visual and haptic feedback for height. It turns out humans can perform nearly optimally at this. Theoretically, Given observations of \(c_{1}\) and \(c_{2},\) and under the assumption that these quantities are independent given \(s\), the posterior over \(s\) is obtained via Bayes’ rule, \(p(s \vert c_{1}, c_{2}) \propto p(c_{1} \vert s) p(c_{2} \vert s)p(s)\).

When the prior is flat and the likelihood functions, \(p(c_{1} \vert s)\) and \(p(c_{2} \vert s)\), are Gaussian with respect to \(s\) with means \(\mu_{1}\) and \(\mu_{2}\) and variances \(\sigma_{1}^{2}\) and \(\sigma_{2}^{2}\), respectively, the mean and variance of the posterior, \(\mu_{3}\) and \(\sigma_{3}^{2},\) are given by the following equations:

\[\mu_{3}=\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}+\sigma_{2}^{2}} \mu_{1}+\frac{\sigma_{1}^{2}}{\sigma_{1}^{2}+\sigma_{2}^{2}} \mu_{2} \\[2ex] \frac{1}{\sigma_{3}^{2}}=\frac{1}{\sigma_{1}^{2}}+\frac{1}{\sigma_{2}^{2}}\]

The important result is: when the prior is flat \((p(s)=\) constant), taking the sum of the two population codes, \(\mathbf{r}_{1}\) and \(\mathbf{r}_{2}\), is equivalent to optimal Bayesian inference. By taking the sum, we mean that we construct a third population, \(\mathbf{r}_{3}=\mathbf{r}_{1}+\mathbf{r}_{2},\) which is the sum of \(\mathbf{r}_{1}\) and \(\mathbf{r}_{2}\) on a neuronby-neuron basis: \(r_{3 i}=r_{1 i}+r_{2 i} .\) The authors also extended this idea to more generalized exponential family of distributions other than just Guassian. A general take-way is that:

The linear combination of PPC is how human brains do Beayesian inference