Stability of Memory Allocation with Neuroidal Model

[  BiologicalComplexity  ] 11 Apr 2021

This is a summary about paper Jacob Beal and Thomas F. Knight, Jr. (2008) Analyzing Composability in a Sparse Encoding Model of Memorization and Association, which is again a follow-up work of paper L. Valiant (2005) Memorization and association on a realistic neural model The two papers talked about a random graph model to understand the basic cognitive tasks like memorization and association in brains.

The question is complicated given following experimental facts:

1. Neurons appear to be sparsely connected. There are \(1.6\times 10^7\) neurons in mouse cortex, but only around 7800 connections. Human cortex has around \(10^{10}\) neurons but only 24000-80000 connections.
2. Most synapses (connections) are quite weak, contributing 0.003 to 0.2 of the firing threshold.

In his 2005 paper mentioned above (see my other blog), Prof. Valiant gave a random graph model consistent with the above parameters to explain memorization and association. As shown in the following figure: Vertices represents neurons and the sparse directed edges are synapses, where each edge has a weight representing its synaptic strength and each node fires when the incoming edges from firing nodes sum to a high enough weight.

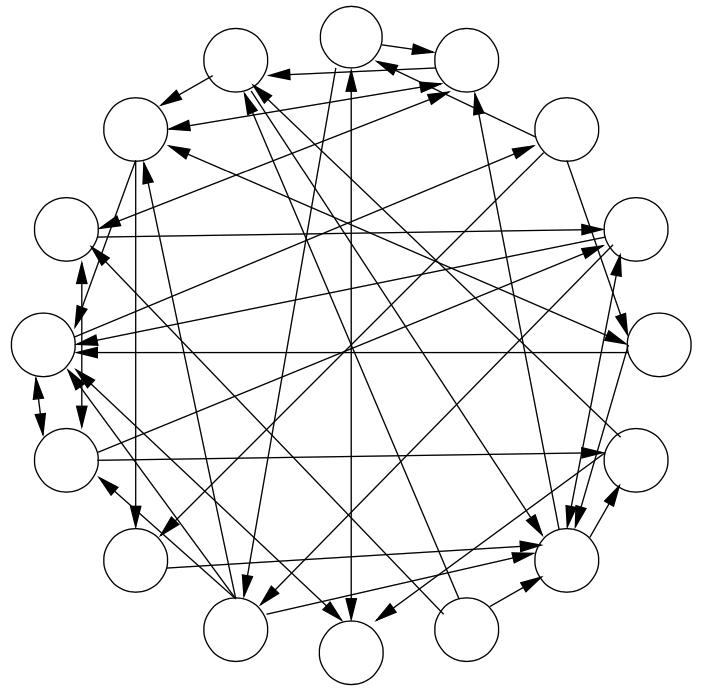
Here are several assumptions:

1. A sparsely firing neuron pattern represents one item
2. When large percentage of the pattern’s neurons fire, say it is recognition.

Memorization and association are abstracted as JOIN and LINK functions separately:

1. Memorization is the joining of two items, A and B, to create a new item C, such that C is recognized if and only if both and A and B are recognized. In one-step JOIN, A and B are triggered to fire simultaneously and C is the nodes they stimulate to fire. In Two-step JOIN, using twice the edge weight, first triggers A, moving nodes that would fire to an intermediate state, then triggers B to fire and C is the intermediate-state nodes that fire.
2. Association is the linking of two items, D and E, such that whenever D is recognized, E is recognized also. D is triggered to fire and the firing is propagated for two steps. In the first step, all edges have weight \(1/k_a\), and in the second step all edges initially have weight 0. LINK works by raising the second-step weight to \(1/k_a\) on edges that arrive at E from firing nodes.

The above model is good that they don’t want to accomplish Join and Link by modifying the graph model more than needed. But fatal weakness still exists. The author of the 2008 paper proposed a property called “composability”, which is to ensure nothing deleterious happens when you chain multiple JOIN LINK operations on top of each other. This kind of stability falls into two parts:

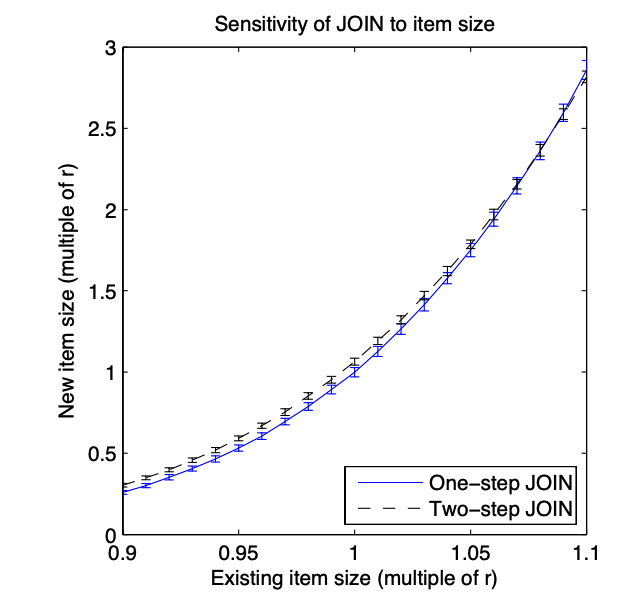
1. Size stability during repeated JOIN memorization. If we keep doing memorizations, we don’t want the new item size get too large or too small. However, it is no case with the current JOIN function, see the following figure: we see that small variations in the size of the initial items are greatly amplified in the size of the item created by the JOIN. The high sensitivity of JOIN to the size of the initial items means that chaining together even a small number of JOIN operations is unstable, and that even a few iterations leads to representations that contain either zero nodes or nearly the entire graph.

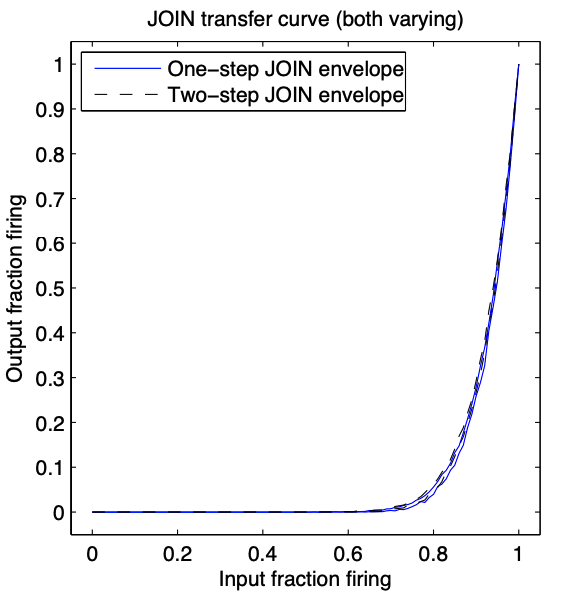
1. Noise sensitivity again in JOIN function. The authors used transfer curves to determine the composability of signals: if appropriate noise margins can be chosen, then signals will be restored as they pass through circuits and noise poses no limit on composability (flat bottom, flat top); Otherwise, the circuits are sensitive to noise and signals can be expected to degrade, perhaps rapidly, as they pass through circuits. And the current JOIN function gives the bad result, as shown in the following figure, no upper noise margin can be established, so even minimal noise will result in significant signal degradation.

Given the above two weaknesses, the author provided two modifications:

1. Add an association stage to the end of a memorization circuit. This removes the size instability problem and steepens the slope of the transfer curve.
2. Lower the firing thresholds km and ka slightly, shifting the transfer curve to provide an adequate noise threshold for firing items.

The author call this JOIN-LINK algorithm, which is simply a composition of the one-step JOIN and LINK algorithms. The new algorithm provides both stable encoding size and good noise margins, allowing unlimited composition with respect to construction and signal propagation.

---

Comments